Na HackYeah 2023 czekało na nas sporo ciekawych wyzwań. Zdecydowaliśmy się podjąć temat niezwiązany z analizą danych - „Quantum Art" 1. W tym artykule postaramy się opowiedzieć, czego udało nam się dokonać podczas Hackathonu i pochwalić się pięknymi obrazkami i gifami 😀
Czym jest Quantum art?
Quantum Art to rodzaj sztuki, w której tworzeniu biorą udział komputery kwantowe. Wykorzystuje się przy tym zjawiska takie jak superpozycja kubitów, splątanie kwantowe, czy fakt, iż komputery kwantowe nie są idealne — ich wyniki obarczone są pewnym błędem.
 Julia set stworzony z liczby wygenerowanej przez komputer kwantowy.
Julia set stworzony z liczby wygenerowanej przez komputer kwantowy.
Znaleźliśmy kilka sposobów na generowanie kwantowej sztuki, większość z nich wykorzystywała komputer kwantowy jako generator liczb losowych.
Komputer kwantowy może generować liczby losowe poprzez dokonywanie pomiaru prawdopodobieństwa stanów w obwodzie kwantowym. Prawdopodobieństwa te obarczone są pewnym błędem pomiaru — stąd możemy traktować je jak liczby losowe. IBM wykorzystał tę metodę do wygenerowania fraktali 2. Postanowiliśmy wykorzystać tę samą metodę do:
- Wygenerowania fraktali w różnych paletach kolorów.
- Animacji kolejnych iteracji tworzenia fraktala (patrz obrazek poniżej).

Fraktale, które tworzyliśmy to zbiory Julii 3. Do ich generowania wykorzystaliśmy funkcję:
def julia_set2CN1(c0=0, c1=0, height=heightsize, width=widthsize, x=0, y=0, zoom=1, max_iterations=100, save=False, cmap='hot'):
# To make navigation easier we calculate these values
x_width = 1.5
y_height = 1.5*height/width
x_from = x - x_width/zoom
x_to = x + x_width/zoom
y_from = y - y_height/zoom
y_to = y + y_height/zoom
# Here the actual algorithm starts and the z paramter is defined for the Julia set function
x = np.linspace(x_from, x_to, width).reshape((1, width))
y = np.linspace(y_from, y_to, height).reshape((height, 1))
z = x + 1j * y
# Initialize the c's to the complex amplitudes obtained from the quantum circuit
c0 = np.full(z.shape, c0)
c1 = np.full(z.shape, c1)
# To keep track in which iteration the point diverged
div_time = np.zeros(z.shape, dtype=int)
# To keep track on which points did not converge so far
m = np.full(c0.shape, True, dtype=bool)
for i in range(max_iterations):
z[m] = (z[m]**2 + c0[m]) / (z[m]**2 + c1[m]) # julia set mating 1
m[np.abs(z) > escapeno] = False
div_time[m] = i
if save:
# Save as png
plt.imshow(div_time, cmap=cmap)
plt.axis('off')
plt.savefig(f'julia_set2CN1_{i}.png', bbox_inches='tight', pad_inches=0)
return div_time
Źródło: Cantorsparadise
Przykładowe fraktale
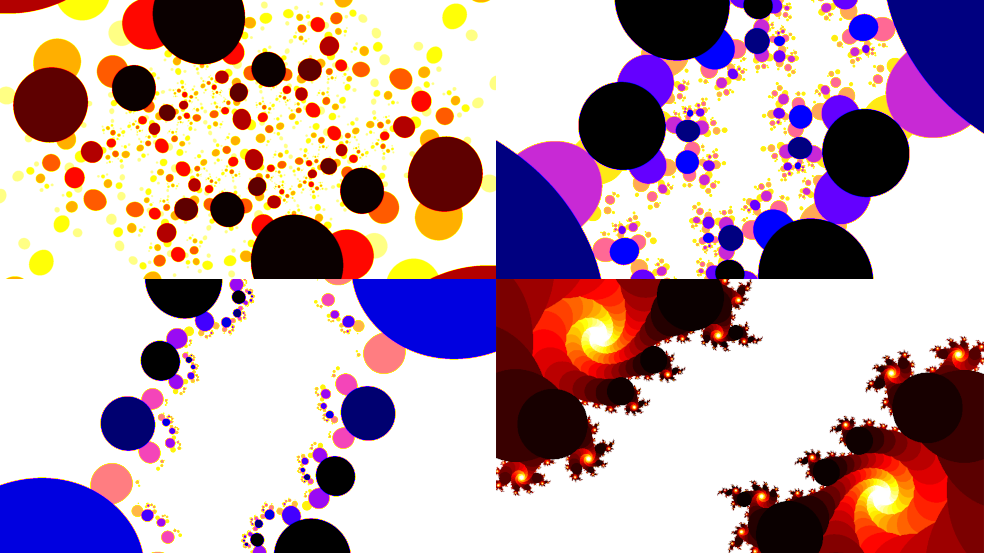
Oto przykładowe fraktale, które wygenerowaliśmy:





A oto ich wersje animowane:




Bibliografia
Artykuł na ten temat: Creating Fractal Art With Qiskit ↩︎
Zbiory Julii: https://pl.wikipedia.org/wiki/Zbi%C3%B3r_Julii ↩︎